Mandelbrot-Sets-Alternate-Parameter-Planes
Original page : Julia and Mandelbrot Sets. Alternate Parameter Planes by David E. Joyce © 1994.
Images of complex quadratic polynomials under
- Geometric transformation
- complex mapping: A complex function f is the transformation function which maps the complex plane z to w
- projection like stereographic projection
z^2+c family
The p-plane is drawn, but initial p parameter is transformed to c:
c = t(p)
So the whole plane (more precisely rectangle viewport) is transformed. For example for c_exponnetial
plane before transformation
xMin = -8.9000000000000004 xMax = 0.7000000000000000
yMin = -2.3999999999999999 yMax = 2.3999999999999999
plane after transformation
xMin = -1.4010186110735179 xMax = 0.6125977074704767
yMin = -0.6754631805511510 yMax = 0.6754631805511510
z^2 + c
First example is the standard plane, simple: c = p
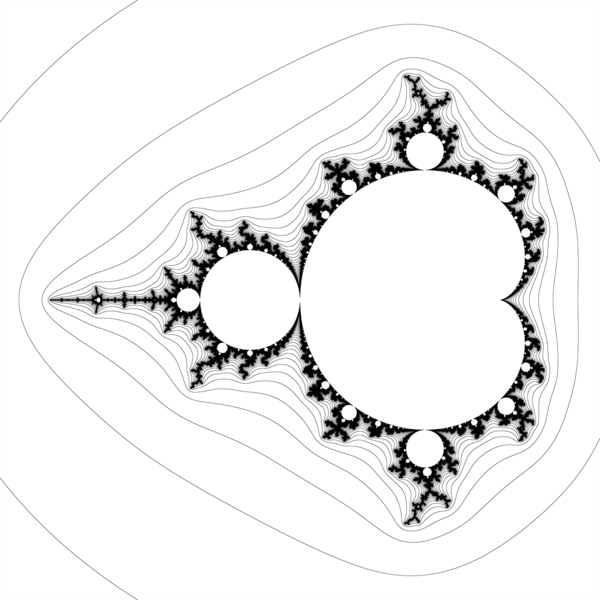
Description by David E. Joyce
the most notable feature of the set is a cardioid.
z^2 + (k +1/p)
Here
c = k + 1/p
so this transformation consist of 2 transformations:
- translation by k
- the inversion with respect to the unit circle centered at zero
Translation is performed before inversion. It moves the set with respect to unit circle and thus changes the shape after the whole transformation
z^2 + 1/p
Second example is simple inversion about a unit circle centered at origin
Here c = 1/p ( and k = 0 so no translatio)
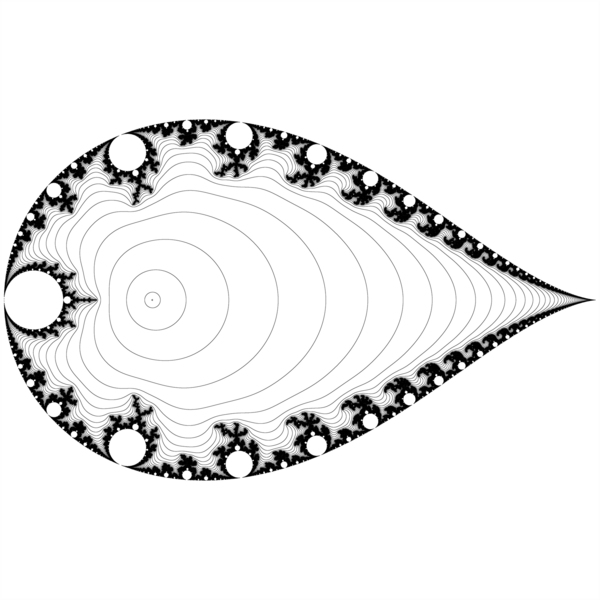
Description by Nikola Ubavić
composition of the inversion with respect to the unit circle centered at zero, and the conjugation (axial symmetry with respect to the real line). The cardioid from the boundary of the Mandelbrot set in the “standard” parameterization corresponds to the tear-shaped curve in the 1/c parameterization.
Description by David E. Joyce
The inverse of the cardioid is the exterior of a teardrop shape. The circles on the outside of the cardioid are inverted to circles on the inside of the teardrop. The cusp of the cardioid becomes the cusp of the teardrop.
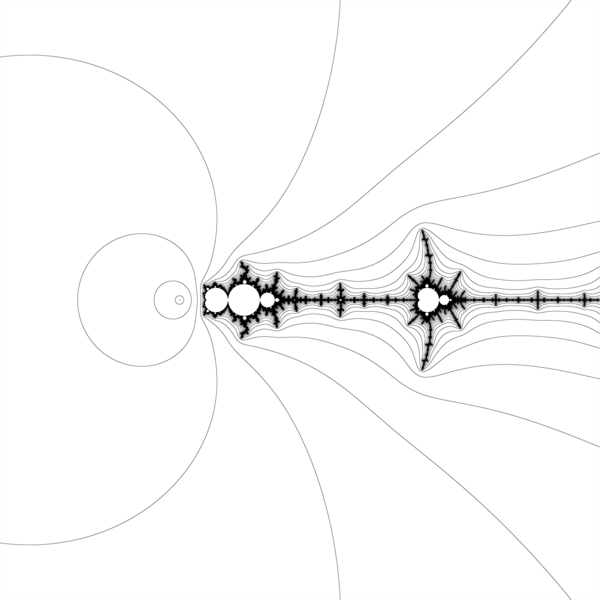
z^2 -2.0+1.0/p
Here : c = -2.0+1.0/p ( and k = -2)
z^2 + 0.25+1.0/p
Here: c = 0.25 + 1.0/p ( and k = 0.25)

Description by Nikola Ubavić
If a 1/4 translation is performed before the inversion, then the cardioid is imaged in a parabola.
The cusp of the cardioid is then moved to the origin, and that inverts to infinity. the cardioid is sent to the outside of a parabola. The circles on the outside of the cardioid are inverted to circles on the inside of the parabola.
Albert Chern:
Since a cardioid is a Möbius inversion of a parabola, you find that the Mandelbrot set is actually a fractal growing along a parabola.
z^2 -1.401155 - 1.0/p
Here: c = -1.401155 - 1.0/p

Exponential map
Here : c = cf + e^p
where
- cf is the Feigenbaum point -1.401155 = Accumulation point of period-doubling
- one can see 7 hyperbolic components for periods 2^0, 2^1, 2^2, 2^3, 2^4, 2^5, 2^6
- note that each componnet has tha same size

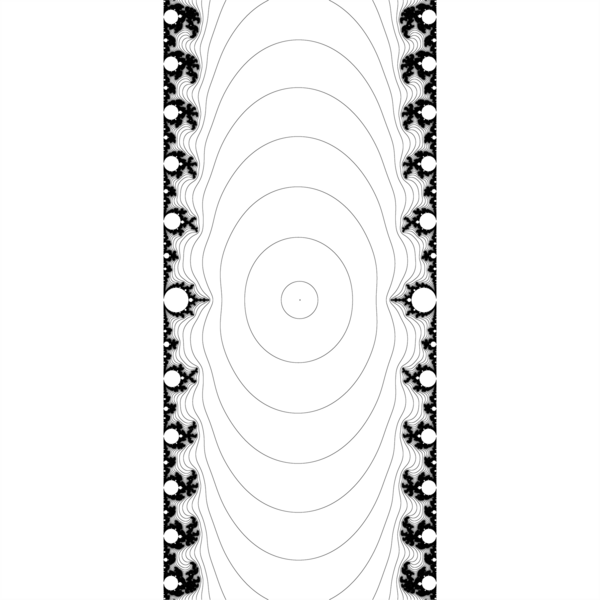
mz(z-1) = logistic family
mz(1.0-z)
so here m = p

z*(1.0-z)/p
here m = 1/p

(1 + 1/p)z(1.0-z)
here m = 1 + 1/p
Animated gif ( click the image to see the animation)
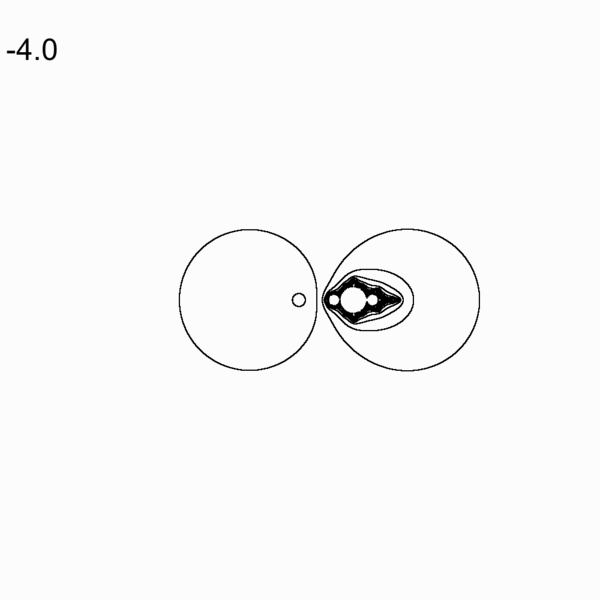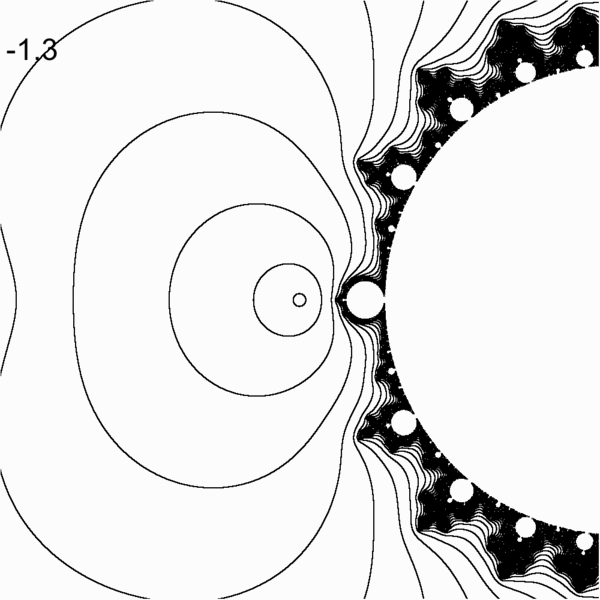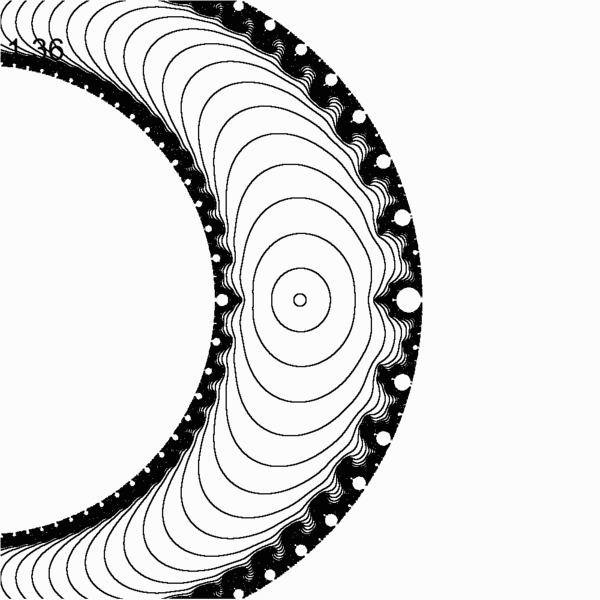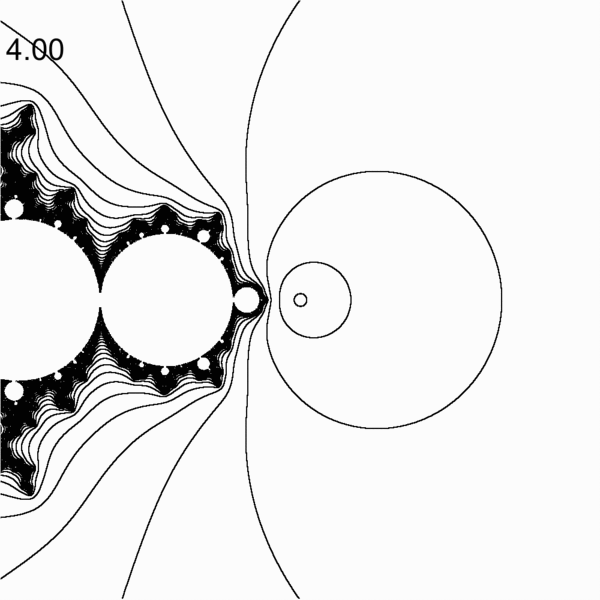
The code for creating gif file is in src/lcm/inversion_gif/ directory
Compare
- changing the inversion offset for the lambda plane mandelbrot by Max Million. Here m = k + 1/p where k is changing from 0 to 2
Code
Families ( forms) of the complex quadratic polynomial
One (complex) parameter familes of quadratic polynomials. Here parameter space is a 2D plane ( complex plane )
complex double f(const FamilyTypeT FamilyType, const double complex z0 , const complex double p ) {
complex double z = z0;
switch(FamilyType){
case c_type : {z = z*z + p; break;} // complex quadratic polynomial, p is changed in give_parameter function
case lambda_type: {z = p*z*(1.0-z); break;} // p is changed in give_parameter function
default: {z = z*z + p; }
}
return z;
}
Algorithms
- LCM = Level Curves Method = first compute level sets of escape time, then find boundaries of level sets ( = level curves ). Here Sobel filter is used
- DEM = Distance Estimation Method
Plane transformations
// transformation = projection = map from p to c or lambda parameter
complex double map_parameter(const ProjectionTypeT ProjectionType, const complex double parameter, const complex double translation){
complex double p;
// plane transformation
switch(ProjectionType){
case identity :{p = translation + parameter; break;} // first translation and then identity
case inversion :{p = translation + 1.0/parameter; break;} // first translation then inverion, 2 transformations
case exponentiation :{p = translation + cexp(parameter) ; break;} // here one can change cf to get different image
default: {p = parameter;}
}
return p;
}
To do
- update DEM ( not works good for exponential map)
- “the image of ∂M under the transformation log(z − c) for a certain c ∈ ∂M. Namely c = -0.39054087 -0.58678790i, the point on the boundary of the main cardioid corresponding to the golden mean Siegel disk. Note the cusp on the main cardoid in the upper right; looking to the left in the figure corresponds to zooming in towards the point c. (It is unknown at this time if ∂M has positive area; although the figure looks quite black in some regions, upon magnification these features resolve into fine filaments, apparently of area zero. “ Frontiers in complex dynamics by Curtis T. McMullen
-
Mercator Mandelbrot Maps by: Anders Sandberg : a logarithmic projection around a point c0: z-> (log( z-c0 ), arg(z-c0)). The idea for this kind of logarithmic map of the set is from David Madore. While it is a bit of a stretch to call it a Mercator projection, it sounds better than just a log scale map. If the Mandelbrot set is assumed to be about meter-sized these zooms reach the size of an atomic nucleus. - transverse Mercator
- Riemann sphere
- Conformal_Warping_Around_The_Cardioid_In_The_Mandelbrot_Set
- distorted Mandelbrot by Ben’s Fractals
- Moebius by Claude
- Artistic Models of the Hyperbolic Geometry by Vladimir Bulatov
- Zⁿ+ A∙Sin(Cᵐ) by Jens-Peter Christensen
- Ultra Fractal 6 - Mandelbrot Set collision by Some dude: Formula: z = z^2 + c + a*(2^c - c^2) with z0=0 and a changing from 1.1 to 5.5 — Morph details: Location: (3 + 0i) Magnification changes from 1.4 to 3.2 Iteration count: 250 Bailout value: 128
Log of the Mandelbrot set. Image 8 from Frontiers in complex dynamics by Curtis T. McMullen

Git
create a new repository on the command line
echo "# Mandelbrot-Sets-Alternate-Parameter-Planes" >> README.md
git init
git add README.md
git commit -m "first commit"
git branch -M main
git remote add origin git@github.com:adammaj1/Mandelbrot-Sets-Alternate-Parameter-Planes.git
git push -u origin main
Local repo
~/Dokumenty/mandelbrot_planes
Subdirectory
mkdir png
git add *.png
git mv *.png ./png
git commit -m "move"
git push -u origin main
then link the images:

gitm mv -f
Remove a file/directory from a Git repository without deleting it from the local filesystem
git rm --cached myfile.log
Single directory and all it’s content
git rm --cached -r ./png
git commit -m "png"
git push -u origin main
Rename directory
git add ./lcm/
git mv ./lcm ./png
git commit -m "png"
git push -u origin main